As usual, here are the notes we used to create the show. We talked about some of this during this episode:

* OpenAI … wow!

* Exponentials … we don’t think in them
** Lily pad
** Bacteria in the bottle
** Chess board
** Paper folding

* Moore’s law
* Kurzweil law of accelerating returns

Punchline … Bacteria in the bottle.
* So where are we now?
* It looks like zero … until it is too late
* Are we at 11:30 … (still need a microscope to see it)
* Are we at 11:45 … (barely see it)

This is really good! This Week in Startups – Audio: E598: Babak Hodjat, Sentient.ai Co-Founder & Chief Scientist (& main inventor of tech behind Siri), is creating artificial intelligence that learns and adapts with our every decision
https://overcast.fm/+JyGaIiAs

Let’s just put our heads in the sand!

Exponentials
* Several mind blowing examples (classics + some fun new ones)
* Sigmoid
* Moore’s law
* Generalized Moore’s law
* Why we don’t think a sigmoid of Moore’s law is going to save us
* kurzweil law of accelerating returns: http://youtu.be/IfbOyw3CT6A

** 15 years to sequence HIV, 31days to sequence sars “People declared the Human Genome Project a failure halfway through, when one percent had been decoded — they said it’d take 700 years. My reaction was, no, we’re almost done. It was finished seven years later.”
* see WaitButWhy screenshots, from this talk: https://vimeo.com/144847615

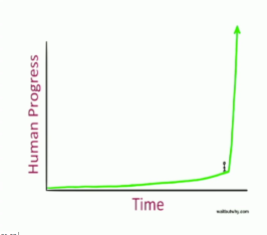
* also animated gif showing how long it appears nothing happens and then the lake fills up all at once
* French children are told a story in which they imagine having a pond with water lily leaves floating on the surface. The lily population doubles in size every day and if left unchecked will smother the pond in 30 days, killing all the other living things in the water. Day after day the plant seems small and so it is decided to leave it to grow until it half-covers the pond, before cutting it back. They are then asked on what day half-coverage will occur. This is revealed to be the 29th day, and then there will be just one day to save the pond. (From Meadows et al. 1972)[3]
* Bacteria in a bottle example: assume they have all the food they need, the only limit is the size of the bottle – start at 11:00am with one bacteria, they double every minute. At 11:01, we have two bacteria. At 11:02, we have four, etc. The bottle fills up at noon. What time was it when the bottle was half full? Yes, 11:59. At 11:45 we could just barely see the bacteria. At 11:30, we still needed a microscope to see it! What time do you suppose the bacteria would start getting concerned about overcrowding? What if we tried to help by bringing in 3 more bottles, giving a total of 4 times as much space. We’d buy them only 2 more minutes!
* 10% growth rate equals doubling in about 7 years
* Diamandis on exponential growth https://www.youtube.com/watch?v=l8ngzUFZQlY Digitization, Deceptive (.01, .02, .04, .08 all look like zero), Disruptive, Dematerialize (smart phone replaces GPS, HD still and video camera, radio, TV, etc), De-monitize (craigslist vs classified ads, uber vs taxi, airbnb vs hotels, etc), Democratize

* Chess board, if $1 on first square, $1 on 2nd, we fill the board with $64. Change the growth rate from 0 to 5% and the board now holds $434. At 20%: $584,000. At 50%: $372 billion. With rice instead of money, doubling every square: 18 quintillion, 446 quadrillion, 744 trillion, 073 billion, 709 million, 551 thousand, 615 – enough rice to pile up to the size of Mt. Everest.

=== Emperor rice on chessboard (wheat on chessboard) ===
From https://en.wikipedia.org/wiki/Wheat_and_chessboard_problem

* 18 * 1 million * 1 million * 1 million … 18,446,744,073,709,551,615
* 2^0 + 2^1 + 2^2 + … + 2^63

“The second half of the chessboard” is a Kurzweil phrase that references the point where an exponentially growing factor begins to have significant economic impact on an organizations’s overall business strategy (wikipedia).

India’s annual rice output is about 1.2 million times as large as the total for the first half of the chessboard (4,294,967,295 … 2^32 – 1).  Around 1,000 times the global production of rice in 2010.

=== Moore’s Law ===
* The number of transistors in a dense integrated circuit doubles approximately every two years.
* Accurate for several decades.
* David House (Intel colleague) concluded that the performance would double every 18 months.

* Moore’s second law.  The cost of a semiconductor fab also increases exponentially over time.

=== Sigmoid (Logistic) function ===

1/(1 + e^-t)

=== Kurzweil ==
From http://www.kurzweilai.net/the-law-of-accelerating-returns

* My view is that the likely outcome is that on the one hand, from the perspective of biological humanity, these superhuman intelligences will appear to be their transcendent servants, satisfying their needs and desires. On the other hand, fulfilling the wishes of a revered biological legacy will occupy only a trivial portion of the intellectual power that the Singularity will bring.